Теория принятия решений

Конспект лекций по курсу «Теория принятия решений»

Введение

Важно отметить, что сложные системы управления как правило, относятся к активным системам, в которых в процессе принятия решения участвует человек как элемент иерархической системы. Действия человека, как элемента системы управления, не могут быть описаны традиционными методами математического моделирования (регрессионными, алгебраическими, дифференциальными, интегральными и другими уравнениями). Великий русский математик Эйлер высказывал такую мысль, что при любом действии, которое совершает человек, он стремится достичь наилучшего результата. Эту мысль можно интерпретировать следующим образом. В процессе деятельности человек решает свою экстремальную задачу. Однако при этом не всегда критерии оптимальности активного элемента и системы управления совпадают.

Наличие активных элементов еще более усложняет проблему управления сложными экономическими системами и делает ее неоднозначно зависящей от участия конкретного человека.

Рассматриваются несколько типов оптимизационных задач управления сложными системами как наиболее характерные и важные для развития народного хозяйства. Такими задачами являются планирование, управление запасами, , транспортные перевозки и ряд других. В дальнейшем мы будем использовать общепризнанную классификацию подобных задач, принятую в теории исследования операций. Для данных классов задач свойственны практически все те особенности сложных систем управления,

Тема 2. Принятие решений в условиях определенности

Под экстремумами функции понимают максимальное и минимальное значение переменной у в упорядоченных парах. Те значения х, при которых значение у принимает максимальное или минимальное значение называются точками экстремумов функции. Две основные теоремы дифференциального исчисления определяют точки экстремумов функций.

Теорема 1. Необходимые условия экстремумов.

Для того, чтобы функция y = f(x) имела экстремум в точке х0 необходимо, чтобы её производная в этой точке равнялась нулю (f’(x0) = 0) или не существовала. Такие точки называются критическими ( или стационарными). Отметим, что эти точки должны входить в область определения функции.

Теорема 2. Достаточное условие экстремума функции.

Если при переходе через точку х0 производная дифференцируемой функции y = f(x) меняет свой знак с плюса на минус, то точка х0 есть точка максимума функции y = f(x), а если с минуса на плюс, то – точка минимума.

Алгоритм исследования функции y = f(x) на экстремум.

Найти производную y’ = f’ (x).

1.  Найти критические точки функции, в которых производная y’= f’ (x) = 0 или не существует.

2.  Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.

3.  Найти экстремумы (экстремальные значения) функции.

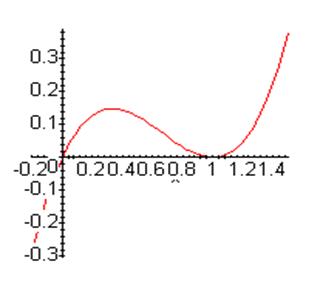
Пример Исследовать на экстремум функцию у = х(х-1)2.

В соответствии с алгоритмом:

1. 

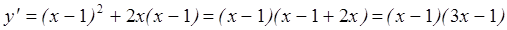
2. 

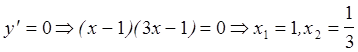
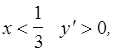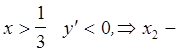3.  При а при точка максимума.

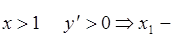При а при точка минимума

4. Находим fmin(1) = 0 fmax(1/3) = 4/27

График исследуемой функции представлен на рис.1.

Рис.1.

Замечание. С помощью дифференциального исчисления возможно находить только экстремумы, находящиеся внутри области определения функции, поскольку в граничных точках области определения производные не существуют, так как нарушена свобода выбора Δх >0 или Δх <0 при вычислении производных. В случае поиска экстремумов на отрезке, необходимо после нахождения экстремумов внутри отрезка вычислить значения функции на границах отрезка. Максимум из значений функции внутри отрезка и на его границах – называется глобальным максимумом, а минимум из значений функции внутри отрезка и на его границах – называется глобальным минимумом.

Пример. Найти глобальный минимум и глобальный максимум функции у = х(х-1)2 на отрезке[-0,2; 1.5].

Локальные минимум и максимум найдены в предыдущем примере. Они равны:

fmin(1) = 0 , fmax(1/3) = 4/27. Найдём значения функции на границах отрезка: f(-0.2) = -0.128, f(1.5) = 3/8.

Глобальный минимум достигается функцией у = х(х-1)2 на границе х = -0,2 и равен –0,128, а глобальный максимум достигается функцией в точке х = 1,5 и равен 3/8.

Линейное программирование

Среди известных разделов математического программирования наиболее развитым и законченным является линейное программирование (ЛП). Современные информационные технологии позволяют достаточно просто реализовать методы ЛП на компьютере. По этой причине данные методы широко используются для решения военных, экономических, промышленных и организационных задач. Это наиболее часто используемый метод оптимизации.

Задачами ЛП называются оптимизационные задачи, в которых целевая функция (критерий оптимизации) и ограничения, представленные в виде равенств и неравенств линейны.

Одним из первых ученых, кто поставил задачу ЛП, был советский ученый, академик, лауреат Нобелевской премии Л. В. Канторович. Его первые статьи с постановкой задачи ЛП и методами ее решения появились в 1938 году. В 1947 году американский ученый Данциг разработал и предложил метод решения задач ЛП ­­- симплекс — метод.

Примеры задач линейного программирования

Задача о диете

На туристской базе имеется n продуктов — Р1, Р2, …,Рn. Есть m питательных элементов. Пусть b1, b2, …, bm — минимальное количество питательных элементов, которое должно содержаться в диете. Необходимо из набора имеющихся на турбазе продуктов составить диету, удовлетворяющую требованиям питательности и имеющую минимальную стоимость.

Введем следующие обозначения. Стоимость одной единицы j-го продукта обозначим через сj, 1 £ j £ n; содержание i-го питательного элемента в единице j-го продукта через aij, 1 £ i £ m, 1 £ j £ n.

Пусть xj — это количество единиц j-го продукта, которое используется в диете, xj ³ 0. Тогда можно записать следующие неравенства:

a11x1+ a12x2 + … + a1nxn ³ b1

a21x1+ a22x2 + … + a2nxn ³ b2

. . . . . . . . . . . . . . . . . . . . . .

am1x1+ am2x2 + … + amnxn ³ bm.

Целевая функция имеет вид:

f = c1x1 + c2x2 +… + cnxn ® min.

Обозначим через A = {aij}, 1 £ i £ m, 1 £ j £ n.

b1 x1 c × × ×

b= × , x = × ; c = × .

bm xn cn

Тогда задачу оптимизации можно записать в матричной форме:

f = cTx ® min,

Ax ³ b,

x ³ 0.

Производственная задача

Имеется производство, выпускающее однородный товар. Запасы m материалов, из которых производится товар известны и равны b1,b2, …, bm. Пусть n — это число различных технологий, по которым данный товар производится из m видов материалов.

Необходимо организовать производство так, чтобы стоимость произведенного товара была максимальной.

Введем следующие обозначения. Пусть сj — стоимость одной единицы товара, произведенной по соответствующей технологии (1 £ j £ n); aij — число единиц i -го материала необходимого для производства единицы j-го товара(1 £ i £ m, 1 £ j £ n); xj — количество единиц изделия, произведенного по j-ой технологии. Тогда справедливы следующие неравенства:

a11x1+ a12x2 + … + a1nxn £ b1

a21x1+ a22x2 + … + a2nxn £ b2

. . . . . . . . . . . . . . . . . . . . . .

am1x1+ am2x2 + … + amnxn £ bm.

Целевая функция имеет вид:

f = c1x1 + c2x2 +… + cnxn ® max.

Тогда задачу оптимизации можно записать в матричной форме:

f = cTx ® max,

Ax £ b,

x ³ 0.

Транспортная задача

Имеется m складов, на которых хранится однородный товар. Запасы товара на складах b1, b2, …, bm соответственно. Имеется n потребителей, потребности которых определяются а1, а2, … , аn. Потребуем, чтобы запас был равен спросу, т. е.должно выполняться равенство:

m n

Sbi =Saj.

i=1 j=1

Надо организовать перевозки товара из складов потребителям таким образом, чтобы затраты на эти перевозки были минимальными.

Обозначим через хij перевозки из i-го склада j-му потребителю. Положим хij ³ 0, т. е. перевозки осуществляются только в одном направлении. Пусть сij — тариф, т. е. стоимость перевозки единицы товара из i-го склада j-му потребителю. Тогда целевую функцию можно записать в виде:

f = c11x11 + c12 x12 +c13x13 +… + cmnxmn ® min.

Далее запишем ограничения. Из каждого склада вывезли весь товар, поэтому справедливы равенства:

х11 + х12 + х13 + … + х1n = b1,

х21 + х22 + х23 + … + х2n = b2,

. . . . . . . . . . . . . . . . . . . . . . . .

хm1 + хm2 + хm3 + … + хmn = bm.

Так как удовлетворили всех потребителей, то выполняются равенства:

х11 + х21 + х31 + … + хm1 = a1,

х12 + х22 + х32 + … + хm2 = a2,

. . . . . . . . . . . . . . . . . . . . . . . .

х1n + х2n + х3n + … + хmn = an.

Матрица коэффициентов ограничений имеет вид:

11…1

11…1

………… 11…1

А = ———————————

1 1 1

1 1 1

. . …………….. . .

1 1 1

Обозначим через

bт=(b1, b2, …, bm, a1, a2, … , an),

xт =( x11, x12, … , x21, x22,…, xmn).

В матричной форме задача имеет вид:

f = cTx ® min,

Ax = b,

x ³ 0.

Задача о банке

Пусть собственные средства в сумме с депозитами составляют b1 денежных единиц(100 млн.$). Часть этих средств, но не менее b2 (35млн.$) должна быть размещена в кредитах. Кредиты являются неликвидными активами банка, так как в случае непредвиденных обстоятельств обратить кредиты в деньги без существенных потерь невозможно.

Ценные бумаги, особенно государственные, можно продать в любой момент. При этом можно получить прибыль или во всяком случае остаться без большого убытка. Поэтому существует правило, согласно которому коммерческие банки должны покупать в определенной пропорции ликвидные активы — ценные бумаги, чтобы компенсировать неликвидность кредитов.

В нашем примере ликвидные ограничения такие — ценные бумаги должны составлять не менее 30 % средств, размещенных в кредитах и ценных бумагах. Пусть х1 — средства(млн.$), х2 — средства, вложенные в ценные бумаги. Тогда имеем систему линейных ограничений:

х1 + х2 £ b1 — балансовое ограничение, (х1 + х2 £ 100)

x1 ³ b2 — кредитное ограничение, (x1 ³ 35)

х2 ³ 0.3(х1+х2) — ликвидное ограничение,

х1 ³ 0, х2 ³ 0.

Цель банка состоит в том, чтобы получить максимальную прибыль от кредитов и ценных бумаг. Поэтому целевая функция имеет вид:

f= c1 x1 + c2 x2 ® max.

Здесь с1 — доходность кредитов, с2 — доходность ценных бумаг. Так как кредиты менее ликвидны, чем ценные бумаги, то обычно с1 > с2. В этом случае линейные ограничения представлены в виде различных неравенств. Задача оптимизации имеет вид:

f= c1 x1 + c2 x2 ® max,

х1 + х2 £ b1,

x1 ³ b2,

х2 ³ 0.3(х1+х2),

х1 ³ 0, х2 ³ 0.

Очевидно, что минимизация целевой функции f равносильна максимизации той же функции, но взятой с противоположным знаком, т. е. — f.

Можно показать, что любая из трех форм задачи ЛП

может быть приведена в другую форму путем некоторого преобразования.

Перейдем от неравенств в ограничениях Ах £ b к равенствам. Для этого введем вектор новых переменных

y = b — Ax ³ 0 . x

Тогда в качестве переменных будет не вектор х, а вектор y и

Ах + y = b.

Аналогично можно получить равенства-ограничения для случая Ах³ b.

Таким образом переход в ограничениях от неравенств к равенствам требует введения так называемых остаточных или избыточных переменных.

Задача ЛП, у которой ограничения записаны в виде равенств называется задачей, представленной в стандартной форме.

Итак, используя стандартную форму задачи ЛП, можно сформулировать основные определения.

1. Допустимое решение задачи представляет собой неотрицательный вектор х, для которого выполняются ограничения Ах = b.

2. Оптимальным решением задачи называется такой допустимый вектор х0, для которого соответствующее ему значение целевой функции f0 = cтх0 больше, чем для любого другого допустимого решения, т. е. х0 является оптимальным решением задачи тогда и только тогда, когда х0ÎS и cтх0 ³ сх для " х Î S, где допустимая область S ={ x½ Ах = b, x³ 0}.

3. Оптимальное значение задачи — это значение целевой функции, соответствующее оптимальному решению, т. е. f0 = cтх0.

4. В случае, если задача имеет более одного оптимального решения, то говорят, что у нее имеются различные оптимальные решения.

5. Если max f(x) ® +¥ или min f(x) ® -¥, тогда задача ЛП имеет неограниченный оптимум.

Геометрическая интерпретация задачи ЛП

Рассмотрим следующий пример:

f = -2×1 + x2 ® min,

x1 + x2 £ 5,

x1 + 2×2 ³ 2 ,

x1 £ 3,

x1 ³ 0, x2³ 0.

Построим область допустимых решений. Каждое из неравенств — ограничений определяет полуплоскости, пересечение которых дает многоугольник (рис.1).Этот многоугольник (выпуклый многогранник) и представляет собой допустимое множество решений S. Если заранее зафиксировать значение целевой функции f, то соответствующие ему точки будут лежать на некоторой прямой. При изменении величины f эта прямая подвергается параллельному переносу.

x2

1

-1 2 3 5 х1

рис.1

В допустимой области содержится бесконечное число допустимых точек. Надо найти допустимую точку с наименьшим значением f(x1,x2). Пусть f(1,1) =-1, тогда график уравнения -2×1 + x2 = -1 представляет собой прямую, проходящую через точки (1/2,0), (0,-1). Прямая, соответствующая значению целевой функции f(2,1) = -3 будет находиться правее данной прямой.

Двигая прямую вправо параллельно самой себе, приходим к такому положению fmin, когда прямая и множество S будут иметь только одну общую точку. Очевидно, что эта точка х0 (3,0) и есть оптимальное решение, а f0 (3,0) = — 6. Заметим, что эта точка оказалась крайней точкой множества S.

Рассмотрим другой пример:

f = 2×1 + 2×2 ® min,

x1 — 2×2 £ 4,

x1 + x2 ³ 1 ,

x1 + x2 £ 6,

x1 ³ 0, x2³ 0.

Вначале строим область допустимых решений S. Получили выпуклый многогранник, изображенный на рис.2.

х2

6

-2 4 6 х1

рис. 2

Прямая, соответствующая значению целевой функции f(2,2) = 8 проходит через точки (4,0), (0,4).

Направление убывания целевой функции показано на рис. 2. Поэтому перемещаем эту прямую вниз до тех пор пока она не сольется с одной из граней многоугольника. В этом случае любая точка на этой грани будет соответствоватиь оптимальному решению. В данном примере мы имеем множество оптимальных решений. Например, точки х(1,0) и х(0,1) являются оптимальными. Им соответствует оптимальное значение целевой функции f0 = 2. В случае, если задача поставлена некорректно в силу неограниченности целевой функции на допустимом множестве решений или противоречивости ограничений, то решение не может быть найдено. В этом случае необходимо провести анализ существующих ограничений и при необходимости изменить их или добавить недостающие ограничения. Рассмотрим следующий пример:

f = 2×1 + 2×2 ® max,

x1 — 2×2 £ 4,

x1 + x2 ³ 1 ,

x1 ³ 0, x2³ 0.

Область допустимых решений имеет следующий вид (рис.3).

х2

1 х1

—

рис.3

Данная задача неразрешима в силу неограниченности целевой функции.

Следующая задача неразрешима в силу противоречивости ограничений (рис.4).

f = 2×1 + 2×2 ® min,

x1 — 2×2 £ 4,

x1 + x2 £ 1 ,

x1 + x2 ³ 6,

x1 ³ 0, x2³ 0.

х2

х1

рис. 4

Симплекс — метод

Геометрическое решение возможно только для двумерных задач ЛП, но далее оно не применимо. Американский ученый Данциг разработал метод, называемый симплекс — методом, который позволяет находить решение задачи ЛП любой размеренности.

Суть вычислительной схемы симплекс-метода состоит в том, что начиная с некоторой допустимой угловой точки осуществляются последовательные переходы от одной допустимой точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.

Рассмотрим задачу ЛП в стандартной форме:

f = cTx ® min,

Ax = b,

x ³ 0.

В этой задаче как правило число уравнений меньше числа уравнений, т. е. решение задачи неединственно. Следовательно выбор наилучшего решения нетривиален.

Представим систему ограничений в каноническом виде:

х1 + а1 m+1 xm+1 +…+ a1S xS + … + a1nxn =b1

х2 + а2 m+1 xm+1 +…+ a2S xS + … + a2nxn =b2

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

хm + аm m+1 xm+1 +…+ amS xS + … + amnxn =bm

Переменные х1, х2, …, хm, входящие с единичными коэффициентами только в одно уравнение системы и с нулевыми в остальные, называются базисными или зависимыми переменными. В канонической системе каждому уравнению сответствует ровно одна базисная переменная. Остальные n — m переменных называются небазисными или зависимыми переменными.

Определение

Базисным решением или опорным планом системы в каноническом виде называется решение, полученное при нулевых значениях небазисных переменных. Например, в данной системе уравнений одно из базисных решений задается как х1 = b1, … , xm = bm, xm+1= … = xn = 0.

Если b1,b2, … ,bm к тому же неотрицательны, то полученное решение называется допустимым базисным решением.

В ЛП справедливы следующие утверждения, которые приведем без доказательства.

1. Если ограничения задачи имеют допустимое решение, то они имеют и базисное решение.

2. Допустимая область является выпуклым множеством.

3. Базисные допустимые решения соответствуют вершинам выпуклого множества.

4. Если целевая функция имеет конечный оптимум, то по крайней мере одно оптимальное решение является базисным. Симплекс-метод, разработанный Данцигом, является вычислительной процедурой, основанной на этих положениях. В линейном программировании справедлива следующая теорема. Если задача ЛП решается с помощью симплекс-метода, то за конечное число шагов будет или получено оптимальное решение или установлена неразрешимость задачи, т. е. симплекс-метод — конечная процедура.

Рассмотрим реализацию этого метода на примере:

f = -2×1 — 4×2 ® min,

3×1+4×2 £ 1700,

2×1+5×2 £ 1600,

x1³0, x2³0.

В стандартной форме задача записывается в следующем виде:

f = -2×1 — 4×2 ® min,

3×1+4×2 +х3 = 1700,

2×1+5×2 + х4 = 1600,

x1³0, x2³0. Так как коэффициенты bi, i=1,2 — положительны, а введенные переменные имеют коэффициенты равные единице, то базисное допустимое решение имеет вид:

х1 =х2=0, х3­=1700, х4 = 1600.

Функция f выражена через небазисные переменные, которые имеют нулевое значение и в этом случае обращается в нуль. Так как х1 и х2 неотрицательны, то их увеличение приведет к уменьшению f, так как коэффициенты при них в f отрицательны. Так можно уменьшить значение функции.

Возьмем одну из переменных х1 и х2 и будем увеличивать ее. У х2 коэффициент в f больше, чем у х1. Поэтому будем изменять эту переменную.

При увеличении х2 значения х3 и х4 тоже будут меняться. При этом надо, чтобы все переменные были больше нуля. Так как

3×1+4×2 +х3 = 1700, х1 =0 как небазисная переменная, то х3 обращается в нуль при х2 = 1700/4 = 425 . Дальше х2 увеличивать нельзя, так как тогда х3 станет отрицательным.

Для второго ограничения 2×1+5×2 + х4 = 1600, х4 обращается в нуль при х2 = 1600/5 = 320. Таким образом мы не можем увеличивать х2 более 320, не нарушая условие х4 ³ 0.

Второе ограничение может быть записано в виде:

(2/5)x1 + x2 +(1/5)x4 = 320.

Умножим это ограничение на 4 и вычтем из первого ограничения, а затем умножив его на -4 вычтем из выражения для f. Таким образом мы исключим х2 из всех уравнений, кроме второго, сделав эту переменную базисной. Тогда получим:

3×1+4×2 +х3 — 4(2/5)x1 — 4×2 -(4/5)x4 = 1700 — 4*320

или

(7/5)x1 +x3 -(4/5)x4 = 420.

Для целевой функции имеем:

-2×1 — 4×2 +4(2/5)x1 + 4×2 +(4/5)x4 = f + 4*320.

Отсюда

— (2/5)x1 +(4/5)x4 = f +1280.

Исходная задача ЛП преобразовалась к виду:

— (2/5)x1 +(4/5)x4 = f +1280,

(7/5)x1 +x3 -(4/5)x4 = 420,

(2/5)x1 + x2 +(1/5)x4 = 320.

Для полученной задачи базисом являются переменные х2 и х3. Небазисными переменными стали х1 и х4. Их значения равны нулю. Тогда значение целевой функции становится равным — 1280.

Далее посмотрим, на сколько можно увеличить х1, чтобы х2 и х3 оставались большими или равными нулю.

Для уравнения

(7/5)x1 +x3 -(4/5)x4 = 420

х3 =0 при х1= 420*5/ 7 = 300.

Для уравнения

(2/5)x1 + x2 +(1/5)x4 = 320

х2 = 0 при х1= 320*5/2 = 800. Поэтому х1 можно увеличить только до 300, оставаясь в допустимой области решений. Исключим х1 из второго ограничения и целевой функции. Для этого запишем его в виде :

х1 + (5/7)x3 — (4/7)x4 = 300.

Вычтем это уравнение, умножив его на 2/5 из второго ограничения. Тогда получим

х2 — (2/7)x3 +(3/7)x4 =200.

Далее вычтем первое ограничение из выражения для целевой функции, умножив его на -2/5. Получим следующее выражение:

(2/7)x3 +(4/7)x4 = f +1400.

Получили каноническую форму задачи с базисом х1, х2:

(2/7)x3 +(4/7)x4 = f +1400,

х1 + (5/7)x3 — (4/7)x4 = 300,

х2 — (2/7)x3 +(3/7)x4 =200.

При допустимом решении х1 = 300, х2 = 200, x3 = x4 = 0 f = — 1400 является минимальным значением целевой функции. Итерационную процедуру нахождения оптимального решения задачи ЛП удобно представить в виде симплекс — таблицы.

Цифры 5 и 7/5 помечены звездочками, так как это коэффициенты при переменных, которые обращаются в базисные.

Обобщим полученные результаты. Предположим, что начальный канонический вид задачи оптимизации задан и что на k — ой итерации получена следующая каноническая форма:

х1 + а¢1 m+1 xm+1 +…+ a¢1S xS + … + a¢1nxn =b¢1

х2 + а¢2 m+1 xm+1 +…+ a¢2S xS + … + a¢2nxn =b¢2

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

хm + а¢m m+1 xm+1 +…+ a¢mS xS + … + a¢mnxn =b¢m

Целевая функция имеет вид:

m с¢m+1xm+1 + с¢m+1xm+1 + … + с¢m+1xm+1 = f — f0,

где f0 = Scibi.

i=1

Здесь переменные х1, …,хm исключены из выражения для f. Запись этих уравнений представим в виде таблицы:

Полученные результаты можно описать итерационной процедурой, состоящей из трех шагов.

1. Найти переменную для включения в базис. Так как переменные хm+1, …, xn являются небазисными, то находим наименьший из коэффициентов cm+1,…, cs, …, cn.

Пусть это коэффициент сs. Если сs < 0, то увеличение хs приведет к убыванию f. По этой причине среди сj < 0 выбирают наибольший по модулю. Это не существенно, но разумно, так как убывание функции происходит быстрее. Если же все сj ³ 0, то значение функции не может быть уменьшено и минимум уже найден. Столбец симплекс — таблицы, в котором находится элемент хS, называется ведущим столбцом.

2. Найти переменную для исключения из базиса. Для этого необходимо определить насколько можно увеличивать хs, не нарушая условие неотрицательности текущих базисных переменных.

Если в i-ом ограничении аis > 0, то наибольшее значение, которое может принимать переменная хS = bi/ аis, иначе переменная хi станет отрицательной. Если аis £ 0, то при увеличении хS базисная переменная хi будет возрастать. Таким образом хS может увеличиваться до значения max хS = min (bi/ аis).

аis > 0

i=1,…,m

Если этот минимум достигается в строке r, то хr обращается в нуль, когда хS принимает значение bi/ аis. Строка, в которой находится элемент аrS называется ведущей строкой, а аrS — ведущим элементом.

3. Построение новой канонической формы. Теперь мы получили новые базисные переменные х1, x2, …, xS, …, xm. xr стала небазисной переменной.

Чтобы построить новую каноническую форму, коэффициент при хS в ведущей строке сделаем равным единице, поделив строку на arS. Затем удалим хS из других ограничений и целевой функции. Для этого из i-ой строки ( i¹r) с хS с коэффициентом аiS вычтем аiS´( новая ведущая строка).

Чтобы преобразовать целевую функцию с коэффициентом сS <0 при хS, вычтем сS´(новая ведущая строка) из строки целевой функции. На (k+1) — ой итерации получим следующую симплекс-таблицу:

Здесь

b*S = b¢r/a¢rS,

a*rS = a¢rj/ a¢rS,

b*i = b¢i — a¢iS b¢r,, i¹r,

a*ij = a¢ij — a¢iS a*rj,

c*j = c¢j — c¢S a*rj,

f*0= f ¢0 + c¢S b*r.

Если надо решать задачу максимизации, тогда либо преобразуют данную задачу в эквивалентную задачу минимизации — f либо в первом пункте итерационной процедуры ведущий столбец выбирается среди сj > 0.

Транспортная задача

Транспортная задача является одной из наиболее распространенных задач линейного программирования и может иметь широкое практическое применение в туристском бизнесе.

Постановка задачи состоит в следующем. Пусть имеется некоторый однородный продукт, который находится у m поставщиков. Обозначим через аi(i=1,…,m) количество продукта, находящегося у i-го поставщика. Этот продукт необходимо доставить n потребителям. Объемы потребления обозначим через bj(j=1,…,n), т. е. каждому j-му потребителю необходимо иметь bj единиц продукта. Надо организовать перевозки так, чтобы они имели минимальные затраты. При этом предполагается, количество продуктов, которое находится у поставщиков равно количеству продуктов, необходимых всем потребителям, т. е. выполняется равенство:

m n

Sai = Sbj. (1)

i=1 j=1

Обозначим через хij — количество груза перевозимого от i — го поставщика j-му потребителю. Очевидно, что хij ³ 0. Пусть стоимость перевозки единицы продукта равна сij. Тогда задача может быть записана следующим образом:

m n

f = SScijxij ® min, (2)

i=1 j=1

при ограничениях

n

Sxij= ai, i=1,…,m, (3)

j=1

m

Sxij = bj, j = 1,…,n, (4)

i=1

xij³ 0, i=1,…,m, j = 1,…,n. (5)

Транспортная задача, в которой суммарные запасы и потребности совпадают, т. е. выполняется условие (1), называется закрытой моделью, в противном случае — открытой. Для открытой модели может быть два случая:

1. Суммарные запасы превышают суммарные потребности, т. е.

m n

Sai > Sbj.

i=1 j=1

2. Суммарные потребности превышают суммарные запасы, т.е.

m n

Sai < Sbj.

i=1 j=1

Открытая модель решается приведением к закрытой модели. Рассмотрим задачу первого типа. Она формулируется следующим образом.

m n

f = SScijxij ® min,

i=1 j=1

при ограничениях

n

Sxij£ ai, i=1,…,m,

j=1

m

Sxij = bj, j = 1,…,n,

i=1

xij³ 0, i=1,…,m, j = 1,…,n.

В этом случае вводится фиктивный потребитель, потребность которого определяется как

m n

bn+1 = Sai — Sbj.

i=1 j=1

Во втором случае задача оптимизации имеет вид:

m n

f = SScijxij ® min,

i=1 j=1

при ограничениях

n

Sxij= ai, i=1,…,m,

j=1

m

Sxij £ bj, j = 1,…,n,

i=1

xij³ 0, i=1,…,m, j = 1,…,n.

Для преобразованию такой задачи к закрытому виду вводят фиктивного поставщика. Тогда

n m

am+1 =Sbj — Sai.

j=1 i=1

Стоимости перевозки единицы продукта фиктивному потребителю и от фиктивного поставщика полагаются равными нулю.

Транспортная задача имеет m+n уравнений с m×n неизвестными. Так как выполняется равенство

m m n n m n

Sai = SSxij =SSxij =Sbj.

i=1 i=1 j=1 j=1 i=1 j=1

то имеем m+n+1 независимых ограничений и следовательно, m+n+1 базисных переменных в допустимом базисном решении. Для транспортной задачи справедлива следующая теорема, которую приведем без доказательства.

Теорема

Транспортная задача всегда разрешима.

Транспортную задачу удобно представить в виде таблицы.

В этой таблице в клетках в левом верхнем углу расположены тарифы, в правом нижнем углу количество груза, которое необходимо перевезти. Сумма произведений элементов каждой клетки — это целевая функция задачи. В нижней строке даны заявки потребителя на грузоперевозки. в последнем столбце определены запасы на складах. В последней клетке таблицы дана сумма, которая определяет равенство (1).

Методы решения транспортной задачи

Метод северо-западного угла

Для нахождения первого базисного решения используется метод

Метод потенциалов

Для транспортной задачи, как и для любой задачи линейного программирования, существует двойственная к ней задача.

Пусть исходная задача имеет вид (1) — (5). Обозначим двойственные переменные для каждого ограничения вида (3) через ui (i=1,…,m) и вида (4) через vj(j=1,…,n). Тогда двойственная задача имеет вид:

m n

Saiui +Sbjvj ® max,

i=1 j=1

ui+vj £ cij, i=1,…,m, j=1,…,n.

Переменные задачи, двойственной к транспортной, ui и vj называются потенциалами. Справедлива следующая теорема.

Теорема

Если решение транспортной задачи является оптимальным, то ему соответствует система из m+n потенциалов, u*i и v*j, удовлетворяющих условиям

u*i + v*j=сij для x*ij>0 ,

и

u*i + v*j£ сij для x*ij=0,

i=1,…,m, j=1,…,n.

Из теоремы следует, что для того, чтобы первоначальное решение было оптимальным, необходимо выполнение следующих условий:

1. Для каждой занятой и отличной от нуля клетки транспортной таблицы сумма потенциалов должна быть равна стоимости единицы перевозки груза, стоящей в этой клетке, т. е.

u*i + v*j=сij. (*)

2. Для каждой незанятой клетки транспортной таблицы сумма потенциалов должна быть меньше или равна стоимости единицы перевозки груза, стоящей в этой клетке, т. е.

u*i + v*j £ сij. (**)

Если хотя бы одна незанятая клетка не удовлетворяет этому условию, то решение не оптимально. Тогда в эту клетку надо переместить некоторое количество груза и ввести этот элемент в базис.

Таким образом для проверки допустимого решения на оптимальность необходимо сначала построить систему потенциалов. Для этого используем условие u*i + v*j=сij. Систему потенциалов можно построить только для невырожденного допустимого решения. Такое решение содержит m+n-1 занятых клеток. Поэтому для него можно составить систему из m+n-1 линейно независимых уравнений вида ui + vj=сij с m+n неизвестными.

Уравнений на одно меньше, чем неизвестных, поэтому система является неопределенной и тогда одному неизвестному ui придают нулевое значение. После этого остальные потенциалы определяются однозначно.

Если известно ui, то vj=cij — ui. Если известно vj, то из того же равенства имеем ui = сij — vj. Итак для данного метода необходимо выполнить следующие шаги.

1. Проверка выполнения оптимальности для незанятых клеток. Просматриваем строки и для каждой незанятой клетки проверяем выполнение условия (**). Если данное условие выполняется, то полученное решение оптимально. Если для некоторых клеток это условие не выполняется, то для каждой такой клетки находим величину (ui + vj) — сij > 0.

2. Выбор клетки, в которую необходимо послать перевозку. Загружается клетка, которой соответствует

max[(ui + vj) -сij].

i, j

3. Построение цикла и определение величины перераспределения груза. Для определения количества единиц груза, котрые необходимо перераспределить, отмечаем знаком “+” незанятую клетку, которую надо загрузить. Находим цикл, все вершины которого за исключением помеченной клетки на ходятся в занятых клетках, причем этот цикл единственный.

Начинаем движение от клетки, отмеченной знаком “+”к другим клеткам, поочередно проставляя знаки “-” и “+”. Затем находим q0=min xij, где xij — перевозки, стоящие в вершинах цикла, отмеченные знаком “-”. Полученная величина q0 определяет, сколько единиц груза можно перераспределить по найденному циклу. Значение q0 записываем в незанятую клетку, отмеченную знаком “+” и двигаясь по циклу, вычитаем из объемов перевозок, расположенных в клетках, которые помечены знаком “-” , и прибавляем к объемам перевозок, находящихся в клетках помеченных знаком “+”.

Если q0 соответствуетнесколько минимальных перевозок, то при вычитании оставляем в соответствующих клетках нулевые перевозки в таком количестве, чтобы во вновь полученном допустимом решении занятых клеток было m+n-1.

4. Проверка нового допустимого решения на оптимальность. Для проверки полученного решения на оптимальность надо вновь построить систему потенциалов и проверить условие оптимальности для каждой незанятой клетки. Если допустимое решение вновь окажется неоптимальным, то следует выполнить вычисления предыдущего пункта. Процесс продолжается до тех пор, пока все незанятые клетки не будут удовлетворять условию (**).

Управление запасами

Задачи создания и управления запасами являются важной проблемой современной науки, так как применяются в различных областях деятельности человека. Возникновение теории управления запасами принято связывать с работами Ф. Эджуорта и Ф. Харриса, появившимися в конце 19 начале 20 веков. В этих работах исследовалась простая оптимизационная модель для определения так называемого экономического размера партии поставки для складской системы с постоянным равномерным расходом и периодическим поступлением хранимого продукта. В течение ряда лет эти исследования оставались незамеченными ни в теоретическом ни в практическом плане. Бурное развитие теории управления запасами началось во время второй мировой войны и продолжилось после нее в рамках науки исследования операций.

Одной из первых задач рассматривалась задача управления запасами, которая учитывала потоки снабжения действующей армии основными материальными ресурсами: боеприпасами, провиантом, горючесмазочными материалами и так далее.

В это время во многих странах для решения подобных задач были привлечены крупнейшие ученые.

После второй мировой войны известная американская фирма RAND CORPORATION создала специальный отдел. В этот отдел были приглашены для работы известные ученые в области прикладной математики со всего мира – Беллман Р, Лэсдон Л. С., Гейл Д, Акоф А, Куликовский Р. и другие. Они разработали основные принципы и методы исследования операций.

Основополагающие разделы исследования операций включают следующие задачи: управление запасами; распределение ресурсов; замена оборудования; задачи недифференцируемой оптимизации (комбинаторные задачи).

Специфика постановки и решения задач исследования операций в отличие от задач классической теории оптимизации состоит в том, что в исследовании операций понятие модель включает составление математической модели, постановку задачи оптимизации и ее решение. В дальнейшем это легко проследить при исследовании задачи управления запасами.

Управление запасами является наиболее разработанным разделом исследования операций и связано с материальными, энергетическими и информационными потоками. Это объясняется тем, что математическими моделями управления запасами может быть описано множество различных реальных ситуаций. В основном это оптимизационные задачи. Функциями цели в таких задачах как правило являются издержки, связанные с созданием, транспортировкой, хранением и возможностью возникновения дефицита. Наиболее простая модель Уилсона и ее модификации успешно применяются во многих отраслях экономики.

Запасом будем называть неиспользуемые в данный момент, но пригодные к применению ресурсы, имеющие экономическую ценность. В качестве запасов могут выступать самые различные физические и экономические категории и объекты: сырье, готовая продукция, оперативные задачи, разработанные туры, номера в гостиницах, забронированные места в транспорте и в театрах, гиды, инструктора на турбазах и т. д.

Запас может пополняться за счет новых поступлений или закупок и уменьшаться с течением времени за счет спроса.

Как известно, создание запасов и их хранение связано с некоторыми затратами, которые, как правило, разбиваются на две группы:

1. Издержки создания запасов.

Эти издержки состоят в наиболее простых случаях из переменной части, зависящей от величины запаса. Чаще всего предполагается, что эти переменные затраты имеют линейный характер и выражают собственно стоимость запасаемой продукции

К(х) = С×х ,

где х — количество приобретаемой продукции, С — стоимость единицы продукции.

Другой составной частью издержек создания запаса является некоторая постоянная величина, возникающая при закупке партии продукции. Сюда обычно включают не зависящие от величины партии расходы: транспортные, административные и т. д. Обозначим такие издержки через СS.

Таким образом общие издержки создания запасов в простейшем случае можно представить в виде:

К(х) = Сх + СS.

2. Издержки, возникающие из-за наличия или отсутствия запасов. Эта статья затрат состоит в свою очередь из целого ряда расходов.

2.1 Затраты на хранение. Сюда относятся как непосредственно расходы на складирование продукции, так и расходы при порче продукции, ее устаревании. Обычно эти издержки принимаются пропорциональными величине запаса в единицу времени:

Т

К(х) = С1òх(t)dt,

0

где С1 — стоимость хранения единицы продукции в единицу времени ; [0,Т] — отрезок времени, на котором решается задача, т. е. период планирования запаса; x(t) — количество единиц продукции в момент времени t, tÎ[0,T].

2.2 Потери, связанные с невозможностью использования средств, вложенных в запасы, например, процент на капитал. Создание запасаемых излишков связано с финансовыми затратами. Эти финансы можно было бы вложить в банк и получить проценты.

2.3 Третья важная статья затрат этой группы связана с отсутствием запасов или, как часто называют, потери из-за дефицита. Часто в задачах по управлению запасами эти издержки принимают пропорциональными разнице между спросом и запасом, т. е.

T

К(х) = С2 ò(x(t) — z(t))dt,

0

где С2 — штраф за неудовлетворенный спрос, т. е. потери, связанные с созданием дефицита единицы продукции в единицу времени, z(t) — реальный запас, х(t) — потребности в ресурсе.

В некоторых задачах управления запасами дефицит недопустим. Например, отсутствие горючего у экскурсионного автобуса во время обслуживания туристов. Тогда штраф С2 полагается равным бесконечно большой величине, то есть С2 = ¥. В этом случае в качестве основного критерия оптимальности можно взять условие максимизации уровня обслуживания, т. е. минимизация вероятности дефицита.

Задача управления запасами состоит в определении такого размера партии приобретаемого ресурса и времени ее поставки, при которых суммарные издержки фирмы, связанные с созданием запаса и его хранением были бы минимальными.

Данная задача не является тривиальной, так как при этом необходимо учесть, что создание большого запаса приводит к возрастанию издержек, связанных с хранением, а при недостаточном запасе увеличиваются потери, связанные с дефицитом ресурса.

При разработке системы управления запасами необходимо учесть, что оптимизационные задачи могут быть многокритериальными..

Классическими являются детерминированные модели с известным спросом в каждый момент времени. Несмотря на достаточную простоту, в настоящее время интерес к таким моделям существенно возрос. Это связано с тем, что в некоторых отраслях промышленности наиболее развитых индустриальных стран проявились организационно-технологические системы с жесткой синхронизацией производственных процессов, которые характеризуются тенденцией к минимизации запасов и в ряде случаев сведения их к нулю (американские системы «Just-in-time», «Material requirement planning», японская система «канбан»).

Модели, используемые при решении задач создания запаса, чрезвычайно разнообразны. Наиболее простая и известная детерминированная модель управления запасами это модель Уилсона, в которой спрос известен и постоянен во времени, издержки хранения пропорциональны количеству хранимого ресурса и интервалу времени, а дефицит недопустим. Требуется определить размер партии продукции и время поставки партии, позволяющие минимизировать затраты на создание и хранение запаса

Как видно из рисунка, существует цикл изменения запаса. Первоначальный запас равен х, а затем происходит его уменьшение за время tS до нуля. Так как мы рассматриваем бездефицитную модель, то как только запас станет равным нулю, должна поступать новая партия продукции такого же размера х и т. д.

Для такой модели оптимальный размер партии продукции, оптимальные значения срока закупки t0s и общих издержек K(x0) определяются формулами

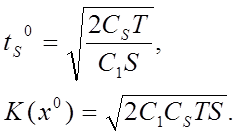Здесь Т— определяет промежуток времени на котором решается задача; S — общий спрос за этот период ; C1 — стоимость хранения единицы продукции в единицу времени; СS — затраты на приобретение и доставку одной партии продукции. На рис. 1.7 приведен график функции издержек при равномерном потреблении ресурса.

Более сложные детерминированные модели связаны с возможностью возникновения дефицита, т. е. отсутствия запаса на складе. На рис.1.8 показана зависимость размера партии и реального количества ресурса от времени. Для такой модели также как и в предыдущем случае существует цикл изменения запаса. В течение времени t1 имеющийся запас уменьшается до нуля. С этого момента начинается накопление невыполненных заказов, т. е. происходит рост дефицита. По истечению времени t2 поступает партия ресурса, которая ликвидирует дефицит и создает запас. Далее запас уменьшается, возникает дефицит и цикл повторяется.

Функция затрат в отличие от предыдущей модели зависит от двух переменных x и z, где х – это размер закупаемой партии, а z— уровень запаса продукции.

Оптимальные размеры партии и запаса, срока поставки партии, минимальные издержки в этом случае находятся по известным формулам:

_

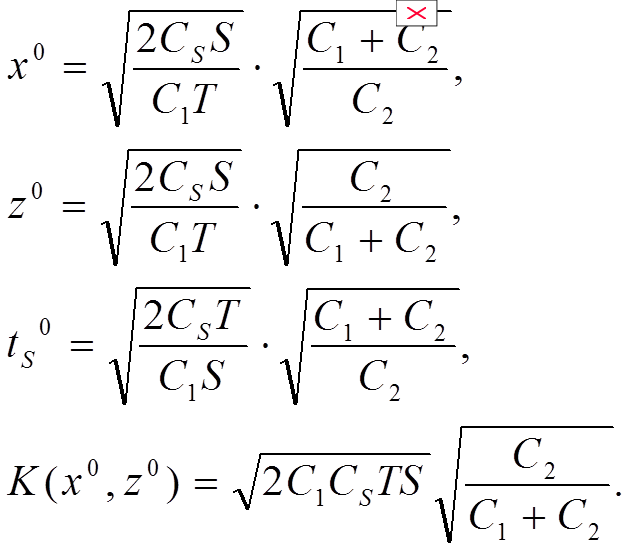Здесь Т, S, С1, Сs имеют тот же экономический смысл, что и в предыдущей задаче, а С2 означает штраф на дефицит единицы ресурса в единицу времени, С2¹¥ ;

Очевидно, что при С2 ® ¥ , выражение для оптимальных значений х0, ts0,К(x0) из формул (1.5) стремятся к значениям х0 , ts0 и K(x0), полученным по формулам (1.4) для модели без учета дефицита.

Так как

то суммарные издержки, полученные в задаче с учетом дефицита меньше, чем в задаче без дефицита. Поэтому в случае, когда значение С2 небольшое, оптимальный уровень запаса должен быть таким, чтобы в некоторый момент времени спрос превышал запас.

Модель Уилсона с постоянным во времени спросом и мгновенным пополнением запаса может быть использована в тех случаях, когда однородный ресурс используется фирмой равномерно, с постоянной периодичностью пополняется, при этом фирма имеет надежных поставщиков запасаемой продукции.

Классическая модель управления запасами с учетом дефицита используется тогда, когда затраты на хранение ресурса более высокие, чем затраты, связанные с дефицитом в течение небольшого промежутка времени

Принятие решений в условиях неопределенности и риска.

Существует множество других различных моделей управления запасами, связанных с конкретными ситуациями и видами систем запасов. Наиболее важной характеристикой модели является вид спроса на запасаемую продукцию. Чаще всего спрос имеет случайный характер, но во многих задачах его можно представить в виде некоторой функциональной зависимости.

Модели, в которых спрос неизвестен, а определены некоторые статистические характеристики, например, распределение вероятностей спроса, являются вероятностными моделями.

В настоящее время все более актуальными становятся модели с вероятностной характеристикой спроса и учетом риска выполнения операций создания запаса. Особый интерес представляют многопродуктовые модели управления запасами, которые должны учитывать некоторые общие ограничения, в частности, на объем складов(холодильников), на возможность транспортных перевозок. Это безусловно усложняет постановку и решение задачи условной оптимизации, так как возникает задача нелинейного программирования с учетом ограничений. Одним из известных решений такой задачи является метод неопределенных множителей Лагранжа. В других, более сложных постановках необходимо использовать методы декомпозиционной оптимизации, которые базируются на идеях системного анализа, изложенных в работах академиков Н. Н. Моисеева, В. В. Кафарова и других ученых.

Большое внимание в настоящее время уделяется стохастическому процессу спроса, при этом в качестве основного аппарата математического моделирования используются управляемые марковские процессы.

Классические вероятностные модели управления запасами значительно более точно, чем детерминированные модели, описывают многие существенные особенности большинства реальных задач. Однако, достигается это, как правило, ценой потери таких важных свойств модели, как простота и наглядность. В этом случае ужесточаются требования к полноте и объему априорной информации, что сильно затрудняет практическое применение таких моделей. По этой причине в последние годы стремление найти компромисс между двумя противоречивыми тенденциями – усложнение моделей управления запасами с целью возможно более полного и адекватного отражения действительности и их упрощение с целью облегчения практических применений – привело к необходимости поиска новых подходов к управлению запасами. Появились исследования, основанные на теоретико-игровых моделях, методах адаптивного управления, методологии теории нечетких множеств. Наиболее перспективными среди таких подходов представляются адаптивные методы.

Существующие в настоящее время модели управления запасами далеко не полностью отвечают практическим потребностям автоматизации управления процессами снабжения. Можно указать несколько основных весьма актуальных с практической точки зрения классов задач, недостаточно изученных современной теорией.

Во-первых, это многономенклатурные модели управления запасами. Большинство существующих в настоящее время моделей являются однопродуктовыми. Среди многопродуктовых задач наиболее изучены различные варианты так называемого метода АВС, определяющего принципы агрегирования продуктов в группы родственных в том или ином смысле продуктов при решении задачи совместного управления запасами многих продуктов. В этом случае многономенклатурность, или что то же, некоторая форма зависимости разных продуктов между собой проявляется в наиболее простой форме — как правило, в виде ограниченности некоторого общего для всех продуктов ресурса (ограниченный объем склада, ограничение на суммарную стоимость всех запасов и т. п.) Очевидно, что при отсутствии зависимости между продуктами задача разбивается на несколько однономенклатурных. Немногочисленные практически реализуемые результаты, полученные в этой области, охватывают простейшие дискретные распределения поставок. Для более общих случаев модели оказываются слишком громоздкими для вычислений..

, способствующих наилучшему функционированию систем снабжения (выбор структуры и правил планирования и стимулирования) и управления запасами. Здесь представляется целесообразным использование методологии теории активных систем.

Многокритериальность задач управления

Важной характерной особенностью большинства задач, возникающих при управлении сложными системами, является наличие множества различных целей, к достижению которых стремятся при решении таких задач. Для каждой из этих целей, а они могут быть как количественные так и качественные, обычно бывает задана некоторая характеристика степени достижения – критерий эффективности. Примерами количественных целей могут быть прибыль, увеличение объема продаж, уменьшение времени простоя служащих компании и т. д. Качественные цели, как правило связаны с самим фактом достижения цели и степень достижения оценивается как 0 или 1.

Таким образом в подобных задачах требуется достичь одновременно экстремума нескольких критериев оптимальности. Поэтому их часто называют многоцелевыми или задачами векторной оптимизации.

В этом случае общий критерий оптимальности может быть представлен в виде вектор-функции:

F(x)=(f1(x), f2(x), … , fi(x), … , fn(x)),

где fi(x) – критерий, характеризующий степень достижения i-ой цели, х — вектор состояния системы. Примеров указанных задач достаточно много: глобальные задачи управления крупными фирмами со сложной структурой, где fi(x) – локальная целевая функция i –ой подсистемы; задача составления оптимального плана, в результате выполнения которого стремятся достигнуть, например, максимума объема продаж, прибыли, качественных показателей обслуживания, минимума себестоимости, затрат и т. д.

Для определенности будем считать, что требуется определить такой вектор Х0 , который обеспечивал бы максимум критериям эффективности

f1(x), f2(x), … , fi(x), … , fn(x), то есть требуется найти

где Х – множество допустимых решений.

Существует два принципиально разных подхода к решению задач векторной оптимизации.

Первый подход связан с объединением множества критериев { f1(x)} в единый скалярный критерий, который может быть представлен как некоторая функция от значений критериев

Fc(x)=j (f1(x), f2(x), … , fi(x), … , fn(x)).

Такая операция называется операцией свертывания векторного критерия. Существует несколько различных видов свертки векторных критериев, каждый из которых отражает определенную концепцию постановки задачи оптимизации. Рассмотрим наиболее распространенные элементарные виды свертки.

Первым и одним из наиболее распространенных способов перехода к скалярному критерию является суммирование или экономический способ объединения критериев. В этом случае в качестве объединенного критерия оптимизации принимается критерий вида:

Совокупность коэффициентов {mi}, обычно называемых коэффициентами приоритетности, должна удовлетворять следующим ограничениям:

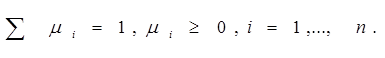Конкретное значение mi определяется при постановке задачи и зависит от важности цели, которая отражается значением критерия fi(x), в общих результатах выполнения оптимизации. При объединении бесконечного числа критериев рассматриваемый способ свертки может быть представлен в интегральной форме:

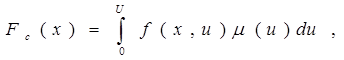где u – непрерывный параметр, uÎ[0, U].

Эта распространенная модификация получается, например, при учете значения критерия оптимальности на некотором интервале времени.

Второй способ перехода к скалярному критерию состоит в введении дополнительных ограничений. В этом случае на значения некоторых критериев совокупности {fi(x)} накладываются ограничения

fi(x)³ fi 0 , 1£ i £ n.

Этот вариант может использоваться и для всех критериев совокупности, то есть для всех i=1,…, n. В этом случае задача максимизации критериев сводится к задаче достижения любой точки множества допустимых решений.

Однако, при использовании данного способа перехода к одноэкстремальной задаче чаще всего в качестве меры достижения цели принимается один из критериев fк(x), а на остальные накладываются ограничения. Выбор значений {fi0} является достаточно произвольным и обычно трудно привести убедительные доводы в пользу того или иного выбора вектора ограничений. В этом случае удобно использование метода экспертных оценок.

Следующий способ перехода к скалярному критерию состоит в обобщенном логическом свертывании критериев. При этом способе свертки критериев обычно рассматриваются два наиболее важных для практики случая. Первый случай определяется тем, что суммарная цель состоит в максимально возможном достижении всех локальных целей:

Fс(x)=min mifi(x), m i³ 0.

1 £ i £ n

Коэффициенты mi имеют тот же смысл, что и в первом способе свертки.

Во втором случае суммарная цель состоит в достижении хотя бы одной из локальных целей:

Fс(x)=mах mifi(x), m i³ 0.

1 £ i £ n

Кроме трех рассмотренных существуют и другие способы преобразования векторного критерия в скалярный, в частности, способ последовательного достижения локальных целей, которые однако не носят такого общего характера, как приведенные выше, и используются при решении ряда специфических задач.

Выше были описаны лишь элементарные способы свертки. В каждой конкретной задаче свертка векторного критерия может быть осуществлена с использованием нескольких элементарных способов.

Например:

Fс(x)= m1f1(x) + m2f2(x), m i³ 0.

fi(x) £ fi 0 , 3£ i £ n,

или

Fс(x)=min (mifi(x) +mi+1fi+1(x)) , m i³ 0.

1 £ i £ n-1

Другой подход к решению задачи векторной оптимизации заключается в решении исходной задачи в ее первоначальной постановке, то есть без перехода к какому-либо скалярному критерию.

Такой подход во многих случаях является более предпочтительным, так как позволяет выбирать окончательное решение не до решения задачи, как это имеет место при свертывании критерия, а уже после получения решения, что часто бывает проще осуществить на практике. В результате решения исходной зри использовании векторного критерия получают некоторое множество Q , называемое множеством эффективных точек, или множеством Парето, или множеством неулучшаемых точек и т. д. Очевидно, что раз множество Q является решением поставленной задачи, то QÌХ, где Х – множество допустимых решений задачи оптимизации.

Рассмотрим двухкритериальную задачу оптимзации, например определения оптимального плана распределенияя ресурсов (рис.2.6). Любому допустимому плану распределения хÎХ соответствует определенное значение локальных критериев f1(x) и f2(x). Множество D определяется множеством значений функций f1(x) и f2(x), которые они принимают при различных хÎХ, то есть множество D представляет собой отображение множества допустимых решений на множество значений локальных целевых функций.

f1(x)

k1

b

k2

D

m1f1 + m2f2

0 f1(x)

Рис.2.6

Северо-восточная граница множества D – k1 k2 – определяет множество эффективных точек Q.

Формально можно дать следующее определение множества эффективных точек:

точка х*ÎQ есть эффективная точка, если не существует другого хÎХ, такого, что

f1(x)³ f1(х * ), 1£ i £ n.

и хотя бы для одного i это неравенство выполняется как строгое.

Физически это означает, что нет таких значений х, при которых все локальные критерии не уменьшались и хотя бы один увеличивался. Поясним это на рис.2.6.

Действительно, если мы находимся в точке а ÎD, но не на линии k1k2, то можно двигаться из нее, оставаясь в допустимой области, в таком направлении, что увеличиваются и f1(x) и f2(x). Найти такое направление допустимого движения из точки b невозможно.

Из рисунка также легко заметить, что любое решение задачи при свертке векторного критерия по первому способу будет принадлежать множеству эффективных точек. Это справедливо при условии выпуклости D и положительности µ1, µ2.

max {m1f1(x) + m2f2(x)},

xÎX

будет достигаться на северо-восточной границе множества D. Это обстоятельство указывает один из способов нахождения множества решений задачи векторной оптимизации путем решения скалярных задач при различных значениях m­i.

Аналогичным образом строится множество эффективных точек для трех и более критериев эффективности. Это множество намного меньше, чем множество всех допустимых решений. Данная задача уже не может быть формализована далее и окончательный выбор решения осуществляется лицом, ответственным за принятое решение.

Теоретико — игровые модели принятия решений

Антагонистическая игра как математическая модель принятия решения в условиях противоположных интересов. Матричные игры. Верхняя и нижняя цена игры. Смешанное расширение матричной игры Основные правила для функции выигрыша в смешанном расширении. Теорема фон Неймана..

Определение решения матричной игры. Аналитический и графоаналитический методы нахождения решения матричной игры. Сведение задачи нахождения решения матричной игры к паре двойственных задач линейного программирования. Примеры экономических задач, моделируемых матричными играми.

Игра n лиц как математическая модель совместного принятия решения в условиях несовпадения интересов. Бескоалиционные игры. Задача распределения ресурсов. Условия равновесности ситуации в смешанных стратегиях в биматричной игре. Ситуации равновесия в биматричных играх формата 2х2.

Коалиции. Характеристическая функция игры n лиц.. Эквивалентность кооперативных игр. Величина кооперативного эффекта коалиции. Существенные и несущественные игры. Дележи. Отношение доминирования дележей и его простейшие свойства. С-ядро. Критерий принадлежности дележа к С-ядру. Задача оптимального распределения прибыли.

Сравнение дележей кооперативной игры проводится на основе введения отношения доминирования дележей. Естественный путь сужения множества дележей основан на их сравнении, которое осуществляется на базе отношения доминирования.

Задача Оценка «силы» держателей акций. Акции некоторой акционерной компании распределены между четырьмя акционерами. Первый акционер обладает 10 всех акций, второй — 20%, третий — — 30%, четвертый – 40%. На общем собрании акционеров решение принимается по прав илу простого большинства. Определить оценку силы акционеров при данной схеме голосования. Составляем все перестановки и находим, что вес игрока не пропорционален количеству его акций.